Een lineaire diofantische vergelijking is een vergelijking in de vorm:

px + qy = z

Waarbij p, q en z gehele getallen zijn en er oplossingen gezocht worden in gehele getallen voor de variabelen _x en _y . Die mogen ook negatief zijn.

Deze vergelijkingen worden bestudeerd in de getaltheorie en er zijn specifieke methoden, zoals het uitgebreide Euclidische algoritme, om ze op te lossen. Een oplossing bestaat alleen als de grootst gemene deler van:
P en Q een deler is van Z.

In Excel is de formule =GCD(P;Q) en de uitkomst MOET hetzelfde zijn als de waarde Z.

Voorbeeld:
60x + 22y = 2 en:
=GCD(60;22) uitkomst is 2

Maar hoe bereken je _x en _y? Een opzet in Excel in onderstaande afbeelding:

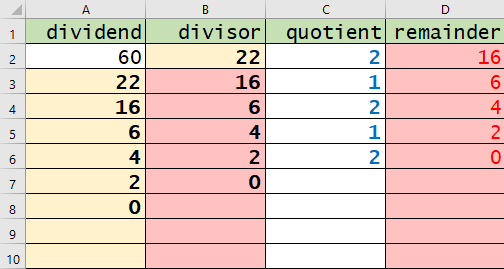
We nemen bovenstaande formule, 60x + 22y = 2. Je deelt telkens de divisor door dividend. M.a.w. hoe vaak gaat de divisor in dividend?
– Helemaal boven aan begin je met dividend (60) en divisor (22).
– 22 gaat 2 keer (dat is de quotient) in 60 en de remainder is 16. Zet die getallen in de cellen C2 en D2.
– Vervolgens vul je divisor 22 bij kolom A in en de remainder 16 in kolom B.
Dat proces herhaal je telkens tot je bij 0 (nul) uitkomt. De een na laatste stap boven 0 is 2. Dat is de grootst gemene deler.
We weten nog dat =GCD(60;22) uitkomst is 2. Dat is gelijk aan de waarde 60x + 22y = 2 en die waarde 2 hebben we in onderstaande tabel berekend. Dat betekent dat we altijd een uitkomst van _x en _y kunnen berekenen en dat gaan we doen.

We zetten twee tabellen op:

In deze tabel zetten we de waarden in [F2] P en in [G2] Q. Tevens de uitkomst van de grootst gemene deler GCD in [J2]. En een getal k (0) in [K2]. Dat getal is nu nog niet belangrijk. Dan nu de tabel waar het echte werk gebeurt.

In rij 12 zet je de getallen 2, 1, 2, 1, 2. Merk op dat dit de getallen (de quotienten) van Kolom C zijn.
Formule in [A13] =F2 en in [A14] de formule =G2. Neem de getallen in kolom B en C (het oranje gedeelte) gewoon over. In elke berekening die je in de toekomst gaat maken volgens dit systeem zullen deze getallen altijd standaard zijn en in die cellen staan. De getallen in het groene en gele gedeelte gaan we nu berekenen:
– (D12 * C13) + B13 = 1. Die uitkomst (1) zet je in D13.
– (E12 * D13) + C13 = 1. Die uitkomst (1) zet je in E13.
Misschien zie je het patroon al:
Het blauwe getal vermenigvuldigen door één cel naar beneden te gaan en vervolgens één cel naar links. Tel daarbij op door nog één keer naar links te gaan. We gaan verder:
– (F12 * E13) + D13 = 3. Die uitkomst (3) zet je in F13.
– (G12 * F13) + E13 = 4. Die uitkomst (4) zet je in G13.
– (H12 * G13) + F13 = 11. Die uitkomst (11) zet je in F13.

Hetzelfde gaan we nu doen om de getallen in rij 14 (groene gedeelte te krijgen. Dus:
– (D12 * C14) + B14 = 2. Die uitkomst (2) zet je in D14.
– (E12 * D14) + C14 = 3. Die uitkomst (3) zet je in E14.
– (F12 * E14) + D14 = 8. Die uitkomst (8) zet je in F14.
– (G12 * F14) + E14 = 11. Die uitkomst (11) zet je in G14.
– (H12 * G14) + F14 = 30. Die uitkomst (30) zet je in F14

De uitkomst voor _x en _y staan ALTIJD in de één na laatste kolom (het gele gedeelte). Het zijn 4 en 11. Die één na laatste kolom geldt voor elke berekening die je ooit gaat maken. Let daar dus op.

Het enige wat je nu nog moet doen is bepalen welke van de twee waarden (4 en 11) negatief is. Daar is geen berekening voor dus dat doe je door ze gewoon in te vullen. Je komt er dan vanzelf achter. Uitkomst moet immers altijd 2 zijn. We vullen eerst –11 in
(60 * 4) + (22 * –11) =. Helaas uitkomst = –2
(60 * –4) + (22 * 11) =. Uitkomst is 2. De waarden voor _x en _y zijn dus –4 en 11.
Zou je geen getal negatief maken is de uitkomst 482. Dat is dus niet goed.

En dan nu . . . wat vertegenwoordigt de k in dit spel? De k vertegenwoordigt een geheel getal, een integer.
Zo’n vergelijking zoals hier getoont kan meerdere oplossingen hebben/accepteren voor _x en _y. Door voor k een ander getal dan 0 (nul) in te vullen kun je andere waarden voor _x en _y krijgen.

Je kunt nu de waarden voor _x en _y invullen in deze tabel en in een formule verwijzen naar deze waarden en controleren of het klopt (uitkomst moet 2 zijn).

Formules kun je in elke willekeurige cel zetten:
Voor x is de formule: =H2 + (G2/J2) * K2 oftewel: =-4 + (22/2) * 0
Voor y is de formule: =I2 – (F2/J2) * K2 oftewel: =11 – (60/2) * 0
Uitkomst MOET ALTIJD 2 zijn.

Let op: In de formule voor y moet je het min-teken zetten – NIET het + teken.
Merk ook op dat je bij waarde x in de formule deelt door G2 (G2/J2) en in de formule voor waarde y deel je door F2 (F2/J2)

Nu kun je voor k een ander getal invullen bijvoorbeeld 8. Dan krijgen _x en _y automatisch de waarden van: 84 en -229. y wordt dus negatief en de uitkomst zal weer 2 zijn. Je kunt zelf een negatief getal invullen voor k.

.